How To Survive If Your Parachute Fails to Open

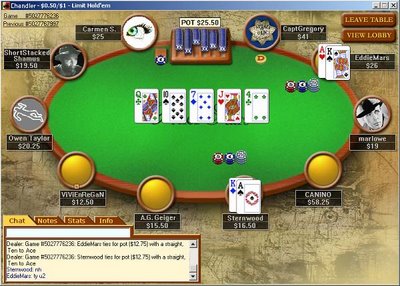
I’m in an online ring game of $.50/$1.00 limit hold ’em. A loose cat limps in early position. Rest of the table folds to me sitting right of the cutoff and I see a pair of ladies looking back. I put in the raise. The cutoff and button both fold. The small blind waits a beat and reraises. Big blind folds. Limper calls. I think about it for a moment then decide just to call and see the flop. Capping ain’t chasin’ anyone and I have position, so I say let’s just buckle up and see what’s what. The pot is an even $5.00.

The out-of-sync rhythm of the small blind’s reraise (combined with earlier info gleaned from playing a few dozen hands with him) adds up to big slick or maybe a pair of hooks. He could have the bullets or cowboys, sure, but something tells me he ain’t got it quite that good. The limper? Could have anything at all.

Flop comes a sweet QT7 rainbow. Both of my opponents check. I bet, the small blind calls, and the limper decides he’ll put his spoon in the dish as well. The pot is now $6.50. As I silently mouth the words “no jack” the turn comes a J. Again, both opponents check. Now what?

How often does this happen? You make a read with confidence, a sequence of events unfolds from which you may potentially benefit from that read, and yet you act otherwise? There I was in the cutoff with my no-longer-pretty set of queens and a feeling of utter certainty that I was up against an opponent slow-playing his straight.

What did I do?

I bet, of course. (“Jingle-brained” ain’t exactly a compliment, if you were wondering.) I cringe as the small blind (inevitably, it seemed) check-raises. Then the madman limper on the other side of the table surprisingly three-bets. What? Has he plugged a gutshot as well (holding K9)? Or maybe he has 98? Criminy.

Do I give up my set? I do potentially have 10 outs here that help me beat a straight (the case queen, three jacks, three tens, and three sevens) -- about 3.5-to-1 against. I’m now looking at a pot of $12.50. It’s $2.00 to call, although I’m a victim of the “sandwich effect” (as Harrington puts it) and so likely it’s gonna cost me another buck to stay in after the small blind caps. That means I’m looking at putting in a total of $3.00 for a shot at $15.50, so the actual pot odds are going to be a little better than 5-to-1.

So math is telling me to stick around. To be honest, I ain’t listening too much to math here. I flopped top set, dammit, and now I’m gonna bust that lucky palooka with the horseshoe up his ass. (After I get lucky and fill up on the river, that is . . . .) So I call (and call) and we have a pot of $18.50 when the river brings a lousy 4.

Poof. Where the hell did I put my Worst-Case Scenario Survival Handbook?

The small blind bets. The limper raises. The pot has grown to a ridiculous $21.50. Practically a small field of cabbage for these stakes. If I fold, I’ve lost a total of $6.00 on this hand. If I make two (or even three) more crying calls as the final round of betting gets capped, I’ll have put in $10.00 altogether. I could calculate pot odds once more and perhaps rationalize that somehow I’m still good here -- or even that I’ve got a 10% shot of being good and so should keep calling -- but that would be strictly non compos mentis. I sigh and let it go. My two friends cap it and it turns out they’re a regular chopper squad with both of ’em holding big slick.

Now there might have been ways I could have lost less on this hand, though I’m not bright enough to see them. Seems more like a cold deck to me, but if anyone has any ideas, I’m all ears. If I were a look-on-the-bright-side type, I might say I “made” $4.00 by folding on the river. (As Miller/Sklansky/Malmuth would put it, folding made my "expectation for the entire hand less negative than the alternatives.") I don’t order my eggs sunny-side up, though. Strictly hard-boiled around here . . . .

Images: The Worst-Case Scenario Survival Handbook (1999), Joshua Piven, David Borgenicht (top); PokerStars screenshot (adapted) (bottom).